----
追記
この記事の計算や表には一部間違いがありました。次の記事の表では直ってるので、そちらをご確認下さい。もしそっちでも間違いがあったら教えてください。
この記事はそれを作るまでに四苦八苦してる時に書いたものです。
----
シャドウバースメンテ来ましたね。私はゴブリンリーダーが大嫌いだったのでナーフとても嬉しいです。一方、豪拳の用心棒や緋色には触れられなかったので、結局2pickではヴァンプがまだ最強じゃないか・・という感じにも思ってます。
あ、tiwtterは@yutakartです。
というわけで久々にブログの記事書いていきますよ。
今回はカードのドロー確率(2pick版)を求めつつ、お勉強と暇つぶしをしようかなと。
手始めに、2コストのカードを引ける確率を求めてみましょう。
条件として、2コスは7枚、先行(1t目に2ドローしない)、初手で1枚も引けなかった場合、全力マリガンで引きにいくということで。2pickなのでデッキは30枚です。
まず、マリガン前の初期手札3枚に、デッキに7枚入っている2コストのカードを最低1枚ドローする確率を求めます。
余事象ってやつですね。1枚も含まれない場合の反対を求めるアレです。
はてな記法のせいで()2重できないんで中学生っぽい書き方になってます
計算式
P1=1-{(30-7)C3/30C3}
=1-(23/30*22/29*21/28) ※計算はExcelでやります[=1-(COMBIN(30-7,3)/COMBIN(30,3))]
=0.564...
この時点で約56%で引けます。
そして、シャドウバースではマリガンしたカードは引かない仕様らしいので、全マリガンしたときに引ける確率を求めましょう。(デッキが27枚になるってだけです)
P2=1-{(27-7)C3/27C3}
=1-(24/27*23/26*22/25)
=0.610...
全マリで61%で引けます。
マリガン終了時点で2コストが引けている確率は、
P=1-{(1-0.56...)*(1-0.61...)}
=0.829...
約83%で引けるみたいです。
そして、ドローするときはマリガンで戻したカードがデッキに戻りますので、2ターン目までの2ドローで引く確率を求めると(引くカードが2枚になります)
P3=1-{(27-7)C2/27C2)}
=1-(24/27*23/26)
=0.459...
2ドローで46%。
つまり2ターン目までに引けている確率は
P4=1-{(1-0.56...)*(1-0.61...)*(1-0.45...)}
=0.907...
約91%で引けるみたいです。
と、こんな感じで作った計算式をExcelの表にしますと

こんな感じでした。
私はポケモンの大文字(命中率85%)という技を、信用できる技として考えていたので、
85%が信用ラインです。
なので、2コストフォロワーの枚数は、先行で85%、後攻で90%の確率で2t目に2コスをプレイできる、6枚が最低ラインだと考えています。
仕方なくこれ以上少なくなってしまうのなら、2コストがプレイできなくても挽回できるカードをデッキに入れたいところです。(ゴブリンブレイカーティナ、豪拳の用心棒、3コストを3/2/3にする、など)
逆に計算してみて意外だったのは、たった3枚しか2コスが無くても61%で引けてしまうところですね。2コスさえ引けてしまえばあとは強いデッキであれば、運が良い人ならそれで勝ててしまいそうですね。
ところで、表の上側の「その後のドロー」の確率は、マリガンで戻したカードを引き直す確率でもあります。
つまり、デッキに2枚入っている「三月ウサギのお茶会」を戻した場合5t目に34.2%、デッキに1枚の「アックスデストロイヤー」を戻すと6t目に22.2%の確率でしか引き直せないことが分かります。
お茶会は間違いなく5t目にプレイしたいカードですから、ぜひキープしたいですよね。
というわけで、マリガンで2コスト以外のカード1枚をキープする場合の表も作りました。
計算式P2の27が28に、3が2になります。(後述する式でまた使います)

87%の確率で2コストもプレイできるように、7枚あると良さそうですね。
6枚だと確率がハイドロポンプに近づいてしまいますw
ちなみに2枚キープの場合
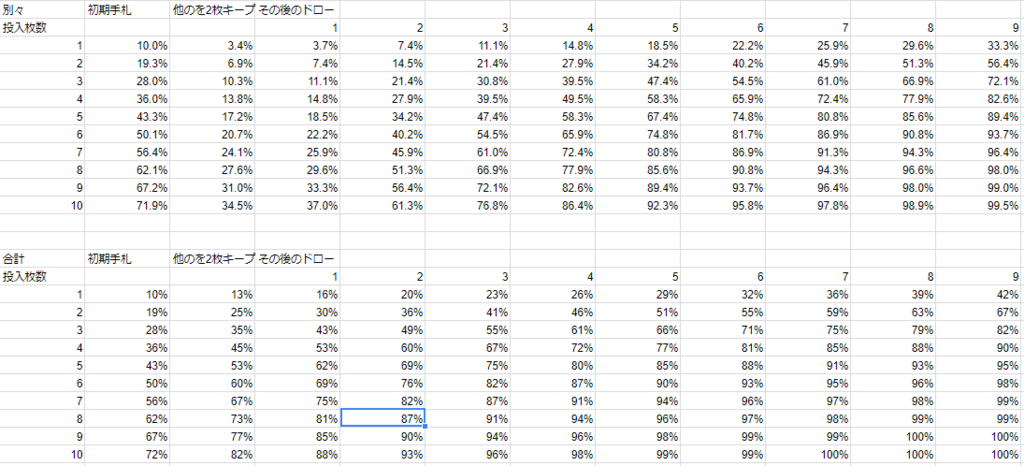
2コストが8枚あれば3,4、3,5の組み合わせみたいなのはキープしても良さそうです。
一応3枚キープの場合も
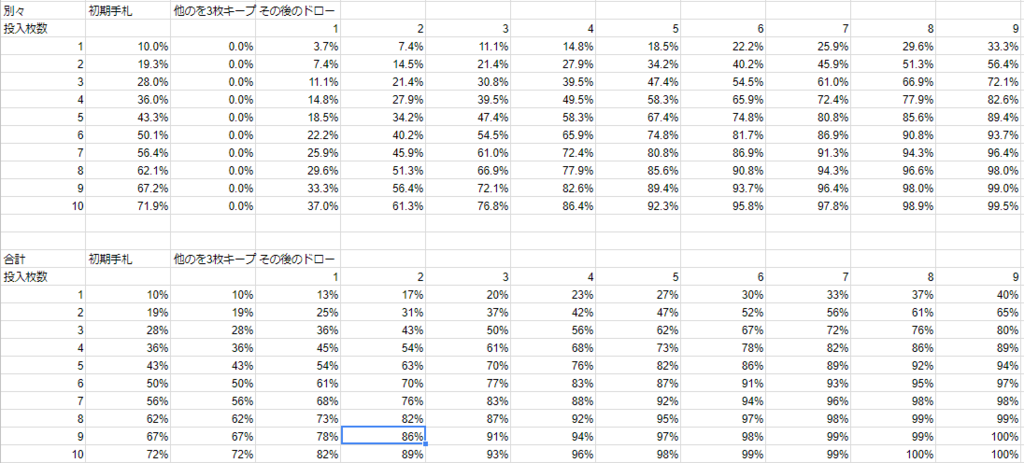
2コスト(の有用フォロワー)が9枚を超えるのはレアケースだと思いますが、その場合は全キープしてても追加のドローで引けそうですね。
次に、2コストのカードを何枚まで積んでも良いか考えてみましょう。
今度は全マリではなく、1枚他のカードをキープする前提で確率を計算します。これは上でも述べたように、お茶会や豪拳の用心棒といったカードをキープしながら2コスを探しに行く場合を考慮しています。
全力で2コスを引くマリガンだと、2コスを引きすぎる確率はもう少し上がります(とはいえその事故が予想されるのであれば2コス狙いは控えめにマリガンされるはずなのでやはり上の前提の表を載せます)
さっきの表の確率は、”最低1枚引く確率”でしたので、これを"最低2枚引く確率"にしてみましょう。
これは、1枚も引かない場合と、n枚の2コス中から1枚だけ引いて残りは他のカードを引く場合の余事象です。
計算式(さっきの式に追加)
P1=1-[{(30-7)C3/30C3}+(7C1*(30-7)C2)/30C3]
12.8%
P2=1-[{(28-7)C2/28C2}+(7C1*(28-7)C1)/28C2] ※1枚キープなので前の式も変わってる
5.6%
P3=1-[(27-7)C2/27C2}+(7C1*(27-7)C1)/27C2)]
6.0%
P4=1-(1-P1)*(1-P2)*(1-P3)
23%
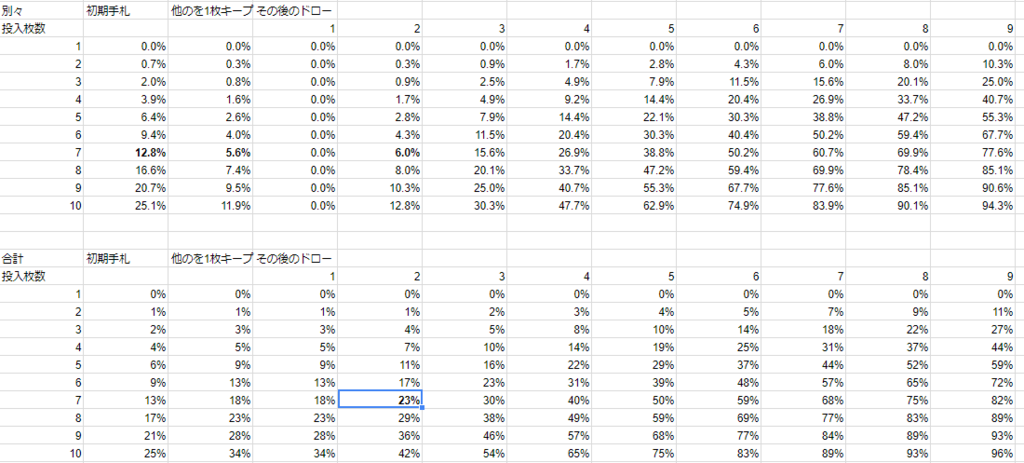
つまり、2コストが7枚で上記のマリガンだと、2ターン目に2コスが1枚以上ある確率は87%で、2枚以上ある確率が23%ということになります。
1枚ちょうどの確率は64%です。
ちなみに2コストが6枚だと、82-17で65%。
5枚だと75-11=64%
8枚だと91-29=62%
2コストフォロワーを2ターン目に1枚だけ引く(その後のプレイはよりマナ通りのプレイが期待できる)という観点からは2コストの枚数は5~8、特に6,7が好ましいと言えますね。
この計算は間違ってたみたいです。詳しく説明するのは難しいんですがExcelで超幾何学分布の関数を使って計算したところ、2枚引き直し前提で2コス7枚でちょうど1枚引ける確率は、5枚で70%、6枚で75%、7枚で79%、8枚で82%、12枚までは増加するものの、増え方は緩やかになっていきます。
また、この数値は、マリガンする前のデッキ構築段階での条件での数値なので、初手に欲しいカードが来てない場合の条件からスタートすると確率は変わります。
せっかくなので、デッキに入れたカードを3枚引いてしまう確率も載せておきます 。
これも2枚の時と同様の条件です。
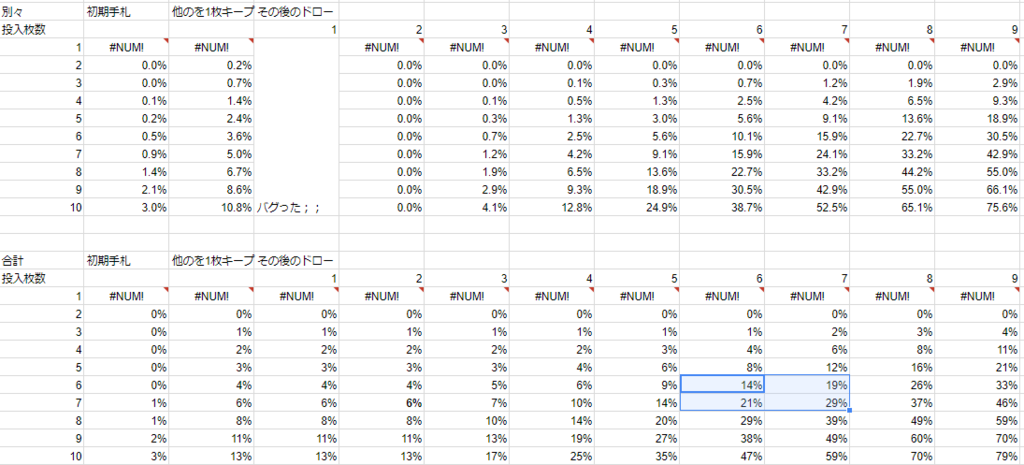
6,7枚の採用でも、6,7ターン目あたりになると2コスを3枚引くリスクが増えてくるって感じですが、その頃までには他のカードでドローしたり、他の有効な行動が見えているといいんじゃないかと思います。
まとめ
カイザやドローソースを引けなければ、2コストフォロワー2枚を一気に使って横に展開する動きをすると、手札がカツカツになってしまいます。
低コストを並べて勝つのは2pickの常套手段ですが、高コストのカードの効果を活かした方が強い盤面になりやすいですし、それらのカードに低コストで対抗すると、下から進化で取ったりしなければならなくなります。
基準である7枚を超える2コストフォロワーをpickする場合、できれば後半に組み合わせて強いカードやドローソースが欲しいですね。
そしてやはり後半に引きすぎるリスクが増えず、マリガンに余裕が生まれる7枚、次点で6枚が理想の枚数だと考えました。1枚キープ時の85%が信用できない人は8枚でもいいのかな。でも後半軽くなるのに耐えられるデッキならいいかも(カラボスとかいるなら軽くしたいよね)
後半の事故率が減る6枚、前半の事故率が減る8枚にもメリットはありますね。
5枚や9枚以上は、かなりリスキーですが、ゴミアミュレットや超パワーカードのせいでやむを得ずその枚数になってしまうのも仕方ないかな、と言った感じでしょうか。
自分の場合、7枚を目指しつつも、ついつい後で来るやろって期待して6枚になることが多いんですが、6枚でも良さそうです。5枚でも後攻ならスペルが実質フォロワーになるからね!
この記事はアプデメンテの暇つぶしで書いたんですけど、2コスト以外のことも考えてpickしていきたいですね~